Kapan uji hipotesis digunakan? Pertanyaan ini krusial bagi peneliti, analis data, dan pengambil keputusan bisnis. Uji hipotesis, sebuah alat analisis statistik yang ampuh, bukan sekadar rumus rumit, melainkan jembatan menuju pemahaman mendalam dari data. Ia membantu kita melangkah dari dugaan spekulatif menuju kesimpulan berbasis bukti. Bayangkan sebuah perusahaan ritel ingin meluncurkan produk baru; uji hipotesis membantu mereka menguji efektivitas strategi pemasaran sebelum investasi besar-besaran. Atau, sebuah lembaga riset kesehatan ingin mengkaji efektivitas obat baru; uji hipotesis menjadi kunci untuk membuktikan atau menyangkal klaim manfaatnya. Singkatnya, uji hipotesis adalah alat yang tak ternilai untuk menguji kebenaran klaim dan membantu kita membuat keputusan yang lebih baik, berdasarkan data yang valid dan teruji.
Dalam dunia yang dibanjiri informasi, kemampuan untuk menyaring informasi yang relevan dan mengolahnya secara ilmiah sangat penting. Uji hipotesis berperan vital dalam proses ini, memungkinkan kita untuk mengambil keputusan yang lebih informatif dan efektif. Dengan memahami berbagai jenis uji hipotesis dan kapan harus menggunakannya, kita dapat meminimalisir bias dan meningkatkan kepercayaan diri dalam pengambilan keputusan. Baik dalam konteks penelitian ilmiah, bisnis, atau kehidupan sehari-hari, kemampuan untuk menganalisis data secara kritis dan membuat kesimpulan yang valid merupakan aset yang berharga.
Uji Hipotesis: Menggali Kebenaran di Balik Data
Dalam dunia yang dibanjiri informasi, kemampuan untuk menganalisis data dan menarik kesimpulan yang valid menjadi semakin krusial. Uji hipotesis hadir sebagai alat penting dalam proses ini, memungkinkan kita untuk menguji klaim atau dugaan (hipotesis) berdasarkan bukti empiris. Baik dalam riset ilmiah, pengambilan keputusan bisnis, atau bahkan dalam kehidupan sehari-hari, uji hipotesis membantu kita melangkah dari spekulasi menuju pemahaman yang lebih objektif.
Bayangkan sebuah perusahaan minuman baru yang mengklaim produknya lebih disukai konsumen daripada merek terkemuka. Klaim ini perlu diuji. Di sinilah uji hipotesis berperan, memberikan kerangka kerja untuk menilai apakah klaim tersebut didukung oleh data atau hanya sekadar asumsi belaka. Melalui pengumpulan data dan analisis statistik, kita bisa menentukan apakah terdapat bukti yang cukup untuk mendukung atau menolak klaim tersebut.
Definisi Uji Hipotesis
Uji hipotesis secara sederhana adalah proses statistik untuk mengevaluasi bukti yang mendukung atau menolak sebuah pernyataan (hipotesis) tentang populasi berdasarkan data sampel. Proses ini melibatkan perbandingan antara apa yang diharapkan (hipotesis) dengan apa yang diamati dalam data. Hasilnya akan memberikan tingkat kepercayaan terhadap hipotesis tersebut.
Contoh Kasus Uji Hipotesis
Sebuah sekolah ingin mengetahui apakah metode pembelajaran baru meningkatkan nilai rata-rata ujian siswa. Mereka mengambil sampel siswa, membagi mereka menjadi dua kelompok (kelompok kontrol dan kelompok eksperimen), dan menerapkan metode pembelajaran baru pada kelompok eksperimen. Setelah ujian, nilai rata-rata kedua kelompok dibandingkan menggunakan uji hipotesis untuk menentukan apakah metode baru tersebut efektif secara signifikan.
Perbandingan Hipotesis Nol dan Hipotesis Alternatif
| Jenis Hipotesis | Definisi | Simbol | Contoh |
|---|---|---|---|
| Hipotesis Nol (H0) | Pernyataan yang menyatakan tidak ada perbedaan atau hubungan yang signifikan antara variabel yang diteliti. Ini adalah pernyataan yang ingin kita tolak atau gagal tolak. | = , ≤, ≥ | Tidak ada perbedaan rata-rata nilai ujian antara kelompok kontrol dan eksperimen. |
| Hipotesis Alternatif (H1 atau Ha) | Pernyataan yang menyatakan adanya perbedaan atau hubungan yang signifikan antara variabel yang diteliti. Ini adalah pernyataan yang ingin kita dukung. | ≠, >, < | Ada perbedaan rata-rata nilai ujian antara kelompok kontrol dan eksperimen. |
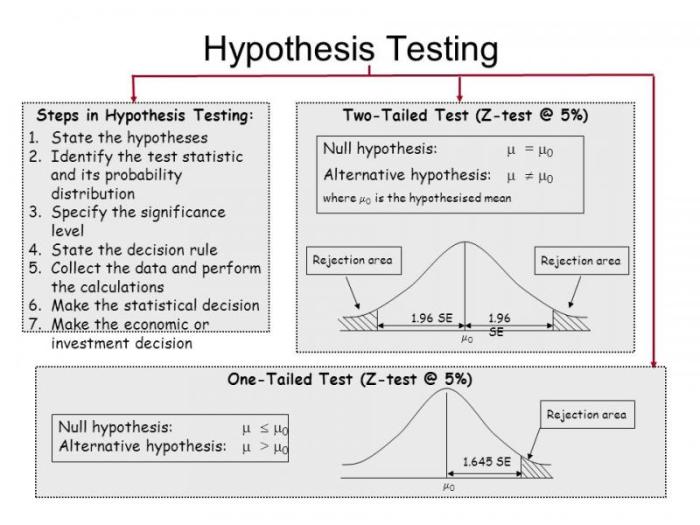
Langkah-Langkah Uji Hipotesis
Uji hipotesis melibatkan beberapa langkah sistematis untuk memastikan hasil yang valid dan dapat diinterpretasikan dengan tepat. Ketelitian dalam setiap tahap sangat penting.
- Merumuskan hipotesis nol (H0) dan hipotesis alternatif (H1).
- Menentukan tingkat signifikansi (α), biasanya 0.05 atau 0.01.
- Memilih uji statistik yang sesuai dengan jenis data dan desain penelitian.
- Mengumpulkan data dan menghitung statistik uji.
- Menentukan nilai p (probabilitas).
- Membandingkan nilai p dengan tingkat signifikansi (α).
- Menarik kesimpulan dan mengambil keputusan apakah menolak atau gagal menolak H0.
Jenis Kesalahan dalam Pengujian Hipotesis
Dalam uji hipotesis, terdapat kemungkinan terjadinya kesalahan. Memahami jenis-jenis kesalahan ini penting untuk menginterpretasikan hasil dengan bijak.
Uji hipotesis, alat analisis data yang krusial, digunakan saat kita perlu membuktikan atau menyanggah suatu dugaan. Bayangkan persiapan pergelaran musik; apakah strategi pemasaran yang diterapkan efektif? Untuk mengetahuinya, kita perlu data penjualan tiket dan tingkat kehadiran penonton. Nah, di sinilah uji hipotesis berperan, membantu kita menganalisis data tersebut, misalnya dengan membaca panduan lengkap di persiapan pergelaran musik untuk mengukur dampak strategi.
Kesimpulannya, uji hipotesis sangat penting untuk pengambilan keputusan berbasis data, tak hanya dalam perencanaan konser, tetapi juga berbagai bidang lain yang memerlukan validasi asumsi.
- Type I Error (kesalahan tipe I): Menolak hipotesis nol (H0) padahal sebenarnya H0 benar. Ini sering disebut sebagai “false positive”. Misalnya, menyimpulkan bahwa metode pembelajaran baru efektif padahal sebenarnya tidak.
- Type II Error (kesalahan tipe II): Gagal menolak hipotesis nol (H0) padahal sebenarnya H0 salah. Ini sering disebut sebagai “false negative”. Misalnya, menyimpulkan bahwa metode pembelajaran baru tidak efektif padahal sebenarnya efektif.
Jenis-jenis Uji Hipotesis
Uji hipotesis merupakan alat statistik krusial dalam berbagai bidang, mulai dari penelitian ilmiah hingga pengambilan keputusan bisnis. Ketepatan pemilihan jenis uji hipotesis sangat menentukan validitas dan reliabilitas kesimpulan yang dihasilkan. Memilih uji yang salah dapat menyebabkan interpretasi data yang keliru, sehingga penting untuk memahami berbagai jenis uji dan kondisi penggunaannya.
Uji t
Uji t digunakan untuk membandingkan rata-rata dua kelompok data. Uji ini sangat serbaguna dan sering digunakan ketika ukuran sampel relatif kecil (kurang dari 30). Terdapat dua jenis utama uji t: uji t berpasangan (paired t-test) yang digunakan untuk membandingkan rata-rata dua pengukuran dari kelompok yang sama, dan uji t tidak berpasangan (independent samples t-test) untuk membandingkan rata-rata dua kelompok yang berbeda. Asumsi utama uji t adalah data berdistribusi normal.
Uji hipotesis, metode andalan peneliti untuk menguji klaim, sering digunakan saat menganalisis data kuantitatif. Pertanyaan muncul, seberapa pentingkah kemampuan matematika, khususnya dalam konteks jurusan akuntansi? Nah, untuk menjawabnya, kita perlu memahami lebih dalam, seperti yang dibahas di apakah jurusan akuntansi harus pintar matematika. Kesimpulannya, pemahaman konseptual matematika krusial, walau tak selalu memerlukan kemampuan berhitung tingkat tinggi.
Kembali ke uji hipotesis, ketepatan penerapannya sangat menentukan validitas kesimpulan penelitian, sehingga pemahaman mendalam sangatlah diperlukan.
Contoh Kasus: Sebuah perusahaan farmasi ingin menguji efektivitas obat baru untuk menurunkan tekanan darah. Mereka membagi peserta menjadi dua kelompok: kelompok perlakuan (menerima obat baru) dan kelompok kontrol (menerima plasebo). Setelah beberapa minggu, mereka membandingkan rata-rata tekanan darah kedua kelompok menggunakan uji t tidak berpasangan.
Uji z
Uji z mirip dengan uji t, tetapi digunakan ketika ukuran sampel besar (biasanya lebih dari 30) atau ketika simpangan baku populasi diketahui. Uji z mengasumsikan data berdistribusi normal dan lebih akurat daripada uji t ketika ukuran sampel besar karena distribusi sampling mendekati distribusi normal.
Contoh Kasus: Sebuah lembaga survei ingin mengetahui apakah persentase pemilih yang mendukung calon tertentu berbeda secara signifikan dari 50%. Mereka mengambil sampel besar dan menggunakan uji z untuk menguji hipotesis ini. Distribusi sampling proporsi akan mendekati distribusi normal karena ukuran sampel yang besar.
Uji Chi-Square (χ²)
Uji chi-square digunakan untuk menganalisis hubungan antara dua atau lebih variabel kategorik. Uji ini memeriksa apakah ada perbedaan signifikan antara frekuensi yang diamati dan frekuensi yang diharapkan. Uji ini tidak mengasumsikan distribusi normal data.
Contoh Kasus: Sebuah restoran ingin mengetahui apakah ada hubungan antara jenis kelamin pelanggan dan jenis makanan yang dipesan. Mereka mengumpulkan data tentang jenis kelamin dan pesanan makanan pelanggan, kemudian menggunakan uji chi-square untuk menguji apakah ada hubungan signifikan antara kedua variabel tersebut.
Uji hipotesis, sebuah metode ilmiah yang krusial, digunakan ketika kita ingin menguji kebenaran suatu dugaan atau prediksi. Bayangkan, kita ingin memahami keagungan Tuhan; mengapa Allah SWT disebut Al-Alim (Maha Mengetahui)? Jawabannya bisa kita telusuri lebih dalam melalui artikel ini: mengapa allah itu al alim sebutkan buktinya. Pemahaman mendalam atas ciptaan-Nya, dari hukum alam hingga kompleksitas kehidupan, seakan-akan menjadi data empiris yang mendukung hipotesis tentang kekuasaan dan pengetahuan-Nya yang tak terbatas.
Kembali ke uji hipotesis, proses ini pun memerlukan data dan analisis yang teliti sebelum kesimpulan dapat ditarik, mirip dengan bagaimana kita mencari bukti kebenaran tentang sifat-sifat Allah SWT.
Uji ANOVA (Analysis of Variance)
Uji ANOVA digunakan untuk membandingkan rata-rata tiga kelompok atau lebih. Uji ini menguji apakah terdapat perbedaan signifikan antara rata-rata kelompok-kelompok tersebut. Asumsi utama uji ANOVA adalah data berdistribusi normal dan varians kelompok sama (homogenitas varians).
Contoh Kasus: Seorang peneliti ingin membandingkan efektivitas tiga metode pembelajaran yang berbeda terhadap prestasi belajar siswa. Mereka membagi siswa menjadi tiga kelompok, masing-masing menggunakan metode pembelajaran yang berbeda, kemudian membandingkan rata-rata prestasi belajar ketiga kelompok menggunakan uji ANOVA.
Tabel Perbandingan Uji Hipotesis
| Jenis Uji | Kondisi Penggunaan | Asumsi |
|---|---|---|
| Uji t | Membandingkan rata-rata dua kelompok, sampel kecil | Data berdistribusi normal |
| Uji z | Membandingkan rata-rata dua kelompok, sampel besar atau simpangan baku populasi diketahui | Data berdistribusi normal |
| Uji Chi-Square | Menganalisis hubungan antara variabel kategorik | Tidak ada asumsi distribusi normal |
| Uji ANOVA | Membandingkan rata-rata tiga kelompok atau lebih | Data berdistribusi normal, varians kelompok sama |
Perbandingan Uji t dan Uji z, Kapan uji hipotesis digunakan
Uji t dan uji z sama-sama digunakan untuk membandingkan rata-rata, tetapi uji t digunakan ketika ukuran sampel kecil atau simpangan baku populasi tidak diketahui, sementara uji z digunakan ketika ukuran sampel besar atau simpangan baku populasi diketahui. Pada sampel besar, perbedaan antara uji t dan uji z menjadi minimal karena distribusi t mendekati distribusi normal.
Alur Kerja Pemilihan Uji Hipotesis
- Tentukan jenis data (kategorik atau numerik).
- Tentukan jumlah kelompok yang akan dibandingkan.
- Periksa asumsi distribusi data (normalitas, homogenitas varians).
- Pilih uji hipotesis yang sesuai berdasarkan jenis data, jumlah kelompok, dan asumsi yang terpenuhi.
Kapan Uji Hipotesis Digunakan?

Pengambilan keputusan berbasis data menjadi kunci keberhasilan di berbagai bidang, mulai dari penelitian ilmiah hingga strategi bisnis. Uji hipotesis berperan krusial dalam proses ini, memberikan kerangka kerja yang sistematis untuk menganalisis data dan menarik kesimpulan yang valid. Dengan uji hipotesis, kita dapat melangkah melampaui sekadar observasi dan masuk ke ranah interpretasi data yang terukur dan teruji.
Situasi yang Membutuhkan Uji Hipotesis
Uji hipotesis bukanlah sekadar prosedur statistik; ia adalah alat yang ampuh untuk menjawab pertanyaan riset yang spesifik. Penerapannya sangat luas, mencakup berbagai situasi di mana data kuantitatif digunakan untuk mendukung atau menolak suatu klaim. Berikut beberapa contohnya:
- Membandingkan efektivitas dua metode pemasaran yang berbeda terhadap penjualan produk.
- Meneliti pengaruh tingkat pendidikan terhadap pendapatan individu.
- Menilai apakah suatu program intervensi berhasil meningkatkan kinerja karyawan.
- Mengukur kepuasan pelanggan terhadap layanan baru yang diluncurkan.
- Menguji apakah terdapat perbedaan signifikan antara kinerja dua kelompok yang berbeda (misalnya, kelompok yang mengonsumsi obat baru dan kelompok plasebo).
Interpretasi Hasil Uji Hipotesis: Kapan Uji Hipotesis Digunakan
Setelah melakukan uji hipotesis, tahap interpretasi hasil menjadi kunci untuk mengambil kesimpulan yang tepat dan bermakna. Memahami nilai p-value, tingkat signifikansi, dan potensi kesalahan merupakan elemen krusial dalam proses ini. Ketepatan interpretasi menentukan kualitas keputusan yang diambil, baik dalam riset ilmiah, analisis bisnis, maupun pengambilan kebijakan publik. Berikut uraian detailnya.
Nilai P-value dan Pengambilan Keputusan
Nilai p-value merupakan probabilitas mendapatkan hasil observasi yang sekurang-kurangnya ekstrem seperti yang diamati, dengan asumsi hipotesis nol benar. Nilai p-value yang kecil (biasanya di bawah tingkat signifikansi yang telah ditentukan) mengindikasikan bukti yang cukup kuat untuk menolak hipotesis nol. Sebaliknya, nilai p-value yang besar menunjukkan bahwa data tidak memberikan bukti yang cukup kuat untuk menolak hipotesis nol. Interpretasi ini penting karena membentuk dasar pengambilan keputusan dalam penelitian.
Penentuan Tingkat Signifikansi (Alpha)
Tingkat signifikansi (α atau alpha) merupakan ambang batas probabilitas yang digunakan untuk memutuskan apakah akan menolak atau menerima hipotesis nol. Nilai alpha umumnya ditetapkan sebesar 0,05 (5%), yang berarti terdapat risiko 5% untuk menolak hipotesis nol meskipun sebenarnya benar (kesalahan Tipe I). Pemilihan nilai alpha bergantung pada konteks penelitian dan konsekuensi dari kesalahan Tipe I dan Tipe II. Penelitian dengan konsekuensi kesalahan Tipe I yang tinggi mungkin menggunakan nilai alpha yang lebih rendah, misalnya 0,01 (1%).
Ilustrasi Hubungan P-value dan Keputusan Hipotesis
Misalkan kita ingin menguji hipotesis bahwa rata-rata tinggi badan mahasiswa di suatu universitas adalah 170 cm. Setelah melakukan uji t, kita memperoleh nilai p-value sebesar 0,03. Dengan tingkat signifikansi 0,05, karena 0,03 < 0,05, kita menolak hipotesis nol. Artinya, terdapat bukti yang cukup kuat untuk menyatakan bahwa rata-rata tinggi badan mahasiswa di universitas tersebut berbeda dari 170 cm. Sebaliknya, jika nilai p-value adalah 0,12, maka kita gagal menolak hipotesis nol karena 0,12 > 0,05. Kesimpulannya, data tidak cukup kuat untuk menyimpulkan perbedaan signifikan dari 170 cm.
Implikasi Kesalahan Tipe I dan Tipe II
Kesalahan Tipe I (false positive) terjadi ketika kita menolak hipotesis nol yang sebenarnya benar. Kesalahan Tipe II (false negative) terjadi ketika kita gagal menolak hipotesis nol yang sebenarnya salah. Kedua kesalahan ini memiliki implikasi yang berbeda. Kesalahan Tipe I dapat menyebabkan pengambilan keputusan yang salah dan berpotensi merugikan, misalnya, meluncurkan produk baru yang sebenarnya tidak laku. Kesalahan Tipe II dapat menyebabkan peluang terlewatkan, misalnya, gagal mengembangkan obat yang efektif karena tidak mendeteksi perbedaan signifikan dalam uji klinis.
Penyajian Hasil Uji Hipotesis yang Efektif
Penyajian hasil uji hipotesis yang jelas dan ringkas sangat penting untuk memudahkan pemahaman pembaca. Berikut beberapa langkah yang dapat diikuti: pertama, jelaskan hipotesis yang diuji dengan jelas. Kedua, laporkan statistik uji yang relevan, termasuk nilai p-value dan tingkat signifikansi. Ketiga, nyatakan kesimpulan berdasarkan hasil uji, apakah hipotesis nol ditolak atau tidak. Keempat, bahas implikasi dari temuan tersebut dalam konteks penelitian. Kelima, presentasikan data dalam bentuk tabel atau grafik yang mudah dipahami.
Batasan Uji Hipotesis
Uji hipotesis, meskipun menjadi alat analisis data yang ampuh, memiliki keterbatasan yang perlu dipahami agar interpretasi hasil tidak menyesatkan. Ketepatan dan efektivitasnya bergantung pada sejumlah faktor, dan mengabaikan batasan ini dapat menghasilkan kesimpulan yang keliru, bahkan menyesatkan kebijakan publik. Memahami batasan ini krusial untuk memastikan interpretasi data yang akurat dan bertanggung jawab, sebagaimana ditekankan oleh para ahli statistika dan metodologi penelitian.
Asumsi dan Keterbatasan Uji Hipotesis
Uji hipotesis bergantung pada sejumlah asumsi, seperti data yang terdistribusi normal, independensi observasi, dan varians yang homogen. Jika asumsi-asumsi ini tidak terpenuhi, hasil uji hipotesis dapat menjadi tidak valid. Contohnya, jika data mengandung outlier yang signifikan, hasil uji t dapat terdistorsi dan menghasilkan kesimpulan yang salah. Lebih lanjut, kekuatan uji hipotesis juga terbatas; uji yang tidak cukup kuat mungkin gagal mendeteksi efek yang sebenarnya ada (false negative), sementara uji yang terlalu kuat dapat mendeteksi efek yang sebenarnya tidak ada (false positive).
Situasi di Mana Uji Hipotesis Tidak Tepat
Terdapat beberapa situasi di mana penerapan uji hipotesis mungkin tidak tepat atau efektif. Misalnya, dalam data dengan ukuran sampel yang sangat kecil, hasil uji hipotesis mungkin tidak memiliki daya statistik yang cukup untuk menghasilkan kesimpulan yang berarti. Selain itu, uji hipotesis kurang efektif dalam menganalisis data non-numerik atau data kualitatif yang kompleks. Penggunaan uji hipotesis pada data yang tidak memenuhi asumsi dasar, seperti data yang tidak terdistribusi normal atau adanya korelasi antar variabel, dapat menghasilkan hasil yang bias dan tidak dapat diandalkan.
Interpretasi Hasil Uji Hipotesis yang Hati-hati
Interpretasi hasil uji hipotesis membutuhkan kehati-hatian ekstra. Nilai p yang rendah (misalnya, di bawah 0.05) tidak selalu menunjukkan hubungan sebab-akibat yang kuat. Korelasi tidak selalu sama dengan kausalitas. Contohnya, penelitian mungkin menemukan korelasi antara konsumsi es krim dan kasus tenggelam, tetapi ini tidak berarti bahwa konsumsi es krim menyebabkan tenggelam. Faktor lain, seperti suhu udara yang panas, mungkin menjadi variabel penentu yang memengaruhi keduanya. Oleh karena itu, penting untuk mempertimbangkan konteks dan faktor lain di luar hasil uji hipotesis.
Pentingnya Konteks dan Faktor Lain
Hasil uji hipotesis hanyalah sebagian kecil dari gambaran yang lebih besar. Konteks penelitian, desain penelitian, dan kualitas data semuanya berperan dalam interpretasi hasil. Mengabaikan konteks dapat menyebabkan kesimpulan yang salah dan menyesatkan. Misalnya, suatu penelitian mungkin menemukan perbedaan yang signifikan antara dua kelompok, tetapi perbedaan tersebut mungkin tidak memiliki arti praktis atau implikasi yang relevan dalam konteks kehidupan nyata. Perlu dipertimbangkan juga faktor-faktor lain seperti bias sampling, efek variabel pengganggu, dan kualitas pengukuran variabel.
Mengatasi Keterbatasan Uji Hipotesis
Meskipun memiliki keterbatasan, penggunaan uji hipotesis tetap penting dalam penelitian. Untuk meminimalkan keterbatasan, peneliti dapat mempertimbangkan beberapa strategi. Pertama, melakukan uji diagnostik untuk memeriksa apakah asumsi uji hipotesis terpenuhi. Kedua, menggunakan uji non-parametrik jika asumsi uji parametrik tidak terpenuhi. Ketiga, meningkatkan ukuran sampel untuk meningkatkan daya statistik. Keempat, mempertimbangkan desain penelitian yang lebih kuat dan metodologi yang lebih komprehensif untuk mengurangi bias dan meningkatkan validitas temuan. Kelima, menginterpretasikan hasil dengan hati-hati dan mempertimbangkan konteks serta faktor lain di luar hasil uji hipotesis itu sendiri. Dengan demikian, penelitian akan menghasilkan kesimpulan yang lebih akurat dan bermakna.
Penutupan

Kesimpulannya, memahami kapan uji hipotesis digunakan adalah kunci untuk mengarahkan penelitian dan pengambilan keputusan yang efektif dan berbasis bukti. Mulai dari menguji efektivitas kampanye pemasaran hingga menilai dampak kebijakan publik, uji hipotesis memberikan kerangka kerja yang terstruktur untuk menganalisis data dan menarik kesimpulan yang valid. Meskipun terdapat batasan dan asumsi yang perlu diperhatikan, kemampuan untuk menginterpretasikan hasil uji hipotesis dengan tepat akan meningkatkan kualitas keputusan yang diambil, mengurangi risiko, dan mengoptimalkan hasil yang diinginkan. Dengan demikian, penguasaan uji hipotesis bukan hanya sekedar kemampuan teknis, tetapi juga sebuah kemampuan kritis untuk bernavigasi di dunia yang semakin kompleks dan didorong data.
 TendikPedia Informasi Mengenai Pendidikan yang Akurat dan Terpercaya
TendikPedia Informasi Mengenai Pendidikan yang Akurat dan Terpercaya