Simetri Lipat Jajar Genjang Pemahaman Mendalam

Simetri lipat jajar genjang, sebuah konsep geometri yang mungkin tampak sederhana, ternyata menyimpan kekayaan yang tak terduga. Dari bentuknya yang khas hingga penerapannya dalam desain dan seni, jajar genjang membuka jendela pemahaman tentang keseimbangan dan pola dalam dunia visual. Memahami simetri lipatnya bukan hanya sekadar menghitung garis bagi, melainkan menyelami aturan-aturan tersembunyi di balik keindahan bentuk. Kajian ini akan mengupas tuntas karakteristik unik simetri lipat jajar genjang, membandingkannya dengan bangun datar lain, dan mengungkap perannya dalam berbagai aplikasi, dari motif batik hingga arsitektur modern. Simak uraian berikut untuk memahami lebih dalam keajaiban geometri sederhana ini.

Bayangkan sebuah jajar genjang, bangun datar yang memiliki dua pasang sisi sejajar. Meskipun tampak sederhana, jajar genjang menyimpan rahasia geometri yang menarik, khususnya terkait simetri lipatnya. Tidak seperti persegi atau segitiga sama sisi yang memiliki banyak garis simetri, jajar genjang memiliki karakteristik unik dalam hal simetri lipat. Kita akan menjelajahi bagaimana sifat-sifat geometri jajar genjang menentukan jumlah dan posisi garis simetri lipatnya, serta bagaimana hal ini berimplikasi pada berbagai aplikasi di dunia nyata. Dengan pemahaman yang mendalam, kita dapat mengapresiasi keindahan dan keunikan bangun datar yang satu ini.

Simetri Lipat Jajar Genjang

Simetri, konsep dasar dalam geometri, merujuk pada keseimbangan visual suatu bangun. Dalam konteks bangun datar, simetri lipat mengacu pada kemampuan bangun tersebut untuk dilipat menjadi dua bagian yang tepat saling menutupi. Memahami simetri lipat, khususnya pada jajar genjang, membuka jendela pemahaman lebih dalam tentang sifat-sifat geometri bangun datar dan aplikasinya dalam berbagai bidang, mulai dari seni hingga arsitektur.

Definisi Simetri Lipat pada Bangun Datar

Simetri lipat terjadi ketika sebuah bangun datar dapat dilipat menjadi dua bagian yang kongruen (identik) melalui sebuah garis. Garis lipatan ini disebut garis simetri. Bangun datar yang memiliki simetri lipat akan memiliki bagian yang saling bercermin terhadap garis simetri tersebut. Bayangkan Anda melipat selembar kertas yang dipotong berbentuk persegi; lipatan yang tepat membagi persegi menjadi dua bagian yang sama persis.

Simetri lipat jajar genjang, dengan dua sumbu simetri yang memotong di tengah, menunjukkan keseimbangan yang tepat. Konsep ini menarik jika kita bandingkan dengan aturan di lingkungan lain, misalnya aturan di sekolah. Memahami apa yang dimaksud dengan tata tertib sekolah, seperti yang dijelaskan di apa yang dimaksud dengan tata tertib sekolah , penting untuk menciptakan lingkungan belajar yang tertib.

Begitu pula dengan simetri lipat jajar genjang, keseimbangannya menciptakan bentuk yang harmonis dan terstruktur, mirip dengan tujuan tata tertib sekolah untuk menciptakan suasana belajar yang kondusif.

Contoh Bangun Datar yang Memiliki Simetri Lipat

Banyak bangun datar yang menunjukkan simetri lipat. Selain persegi yang telah disinggung sebelumnya, contoh lainnya termasuk persegi panjang, lingkaran (memiliki tak terhingga garis simetri), segitiga sama kaki, dan segitiga sama sisi. Namun, tidak semua bangun datar memiliki simetri lipat. Contohnya, segitiga sembarang dan trapesium umumnya tidak memiliki simetri lipat.

Simetri lipat jajar genjang, sebuah konsep geometri sederhana, ternyata menyimpan kompleksitas yang menarik. Memahami sifat-sifatnya membutuhkan ketelitian dan pemahaman mendalam, layaknya profesi guru yang menuntut kesabaran dan dedikasi. Profesi mulia ini, seperti yang dijelaskan di guru merupakan pekerjaan di bidang pendidikan, membutuhkan penguasaan materi yang kuat. Analogi dengan jajar genjang? Sama-sama memiliki struktur dasar yang bisa diurai menjadi elemen-elemen penting.

Kembali ke simetri lipat jajar genjang, menemukan sumbu simetrinya adalah kunci untuk memahami keseluruhan bentuknya.

Perbandingan Simetri Lipat Berbagai Bangun Datar

Tabel berikut memberikan perbandingan simetri lipat beberapa bangun datar, termasuk jajar genjang. Perbedaan jumlah garis simetri dan karakteristiknya mencerminkan sifat geometri masing-masing bangun.

Nama Bangun Datar	Jumlah Simetri Lipat	Garis Simetri	Contoh Ilustrasi
Persegi	4	Dua garis diagonal dan dua garis yang membagi sisi-sisi yang berhadapan	Bayangkan sebuah persegi yang dibagi menjadi dua bagian yang sama persis oleh garis-garis tersebut. Setiap bagian merupakan cerminan dari bagian lainnya.
Persegi Panjang	2	Dua garis yang membagi sisi-sisi yang berhadapan	Mirip dengan persegi, namun hanya memiliki dua garis simetri, yang membagi bangun menjadi dua bagian identik.
Segitiga Sama Sisi	3	Tiga garis yang menghubungkan setiap titik sudut dengan titik tengah sisi di hadapannya	Setiap garis simetri membagi segitiga menjadi dua segitiga yang kongruen.
Jajar Genjang	0	Tidak ada	Tidak ada garis yang dapat melipat jajar genjang menjadi dua bagian yang sama persis dan saling menutupi.

Karakteristik Khusus Simetri Lipat Jajar Genjang

Jajar genjang, berbeda dengan bangun datar lainnya yang telah disebutkan, tidak memiliki simetri lipat. Hal ini merupakan karakteristik uniknya. Ketiadaan simetri lipat ini berkaitan langsung dengan sifat-sifatnya yang memiliki sisi-sisi berhadapan yang sejajar dan sama panjang, tetapi sudut-sudutnya tidak semuanya sama besar (kecuali jika merupakan persegi panjang khusus).

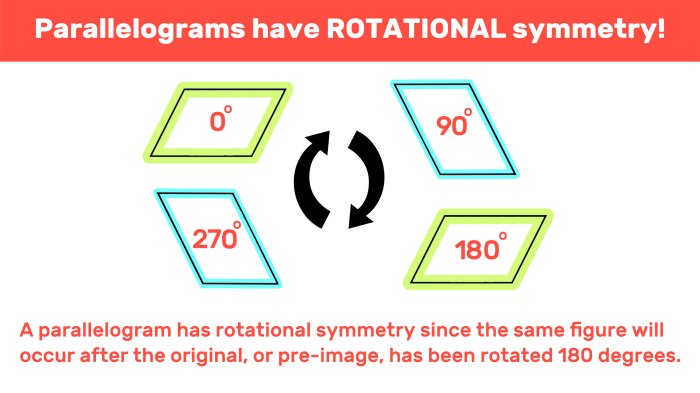
Perbedaan Simetri Lipat dan Simetri Putar pada Jajar Genjang

Simetri putar mengacu pada kemampuan bangun untuk diputar pada suatu titik pusat dan tetap terlihat sama. Jajar genjang memiliki simetri putar tingkat 2, artinya ia terlihat sama setelah diputar 180 derajat. Ini berbeda dengan simetri lipat yang melibatkan lipatan, dan jajar genjang, seperti yang telah dijelaskan, tidak memiliki simetri lipat.

Simetri lipat jajar genjang, konsep geometris yang sederhana namun elegan, ternyata menyimpan kaitan menarik dengan dunia seni. Bayangkan garis-garis simetri yang membagi bentuk tersebut secara presisi; demikian pula ketepatan gerakan dalam tari. Gerakan tari yang indah, menurut gerakan tari harus dilakukan dengan kekuatan dan kehalusan, mencerminkan keseimbangan dan harmonisasi, mirip dengan simetri yang terlihat pada jajar genjang.

Pemahaman simetri ini dapat meningkatkan apresiasi terhadap estetika dan keindahan gerakan tari, mengungkap kedalaman yang tersembunyi di balik setiap langkah. Kembali ke jajar genjang, kita bisa melihat bagaimana konsep simetri ini bisa diinterpretasikan secara kreatif dalam berbagai bidang.

Sifat-Sifat Simetri Lipat Jajar Genjang

Jajar genjang, bangun datar yang didefinisikan oleh dua pasang sisi sejajar, memiliki karakteristik geometri unik yang berkaitan dengan simetri lipatnya. Memahami sifat-sifat ini penting untuk mengklasifikasikan dan menganalisis bangun datar tersebut dalam berbagai konteks, mulai dari ilmu ukur hingga desain arsitektur. Keberadaan atau ketidakhadiran garis simetri lipat secara langsung memengaruhi sifat-sifat geometri jajar genjang dan menentukan bentuknya yang khas.

Lima Sifat Geometri Jajar Genjang dan Simetri Lipatnya

Jajar genjang, berbeda dengan persegi atau persegi panjang, memiliki keterbatasan dalam hal simetri lipat. Berikut lima sifat geometri yang berkaitan erat dengan keterbatasan tersebut:

1. Sisi-sisi yang berhadapan sejajar dan sama panjang. Sifat ini memastikan bahwa jika terdapat garis simetri, ia harus membagi jajar genjang menjadi dua bagian yang identik, dengan masing-masing bagian mencerminkan bagian lainnya.
2. Sudut-sudut yang berhadapan sama besar. Ini berarti bahwa garis simetri, jika ada, harus membagi sudut-sudut yang berhadapan menjadi dua bagian yang sama besar.
3. Diagonal-diagonalnya saling membagi dua. Walaupun diagonal tidak selalu merupakan garis simetri, sifat ini memberikan informasi penting tentang kesimetrisan internal jajar genjang.
4. Jumlah sudut dalam jajar genjang selalu 360 derajat. Sifat ini, meskipun tidak secara langsung terkait dengan simetri lipat, membatasi kemungkinan jumlah dan posisi garis simetri.
5. Luas jajar genjang dihitung dengan mengalikan panjang alas dengan tinggi. Meskipun tidak secara langsung berkaitan dengan simetri lipat, rumus ini menunjukkan bagaimana bentuk jajar genjang, yang dipengaruhi oleh simetrinya, menentukan luasnya.

Pengaruh Sifat-Sifat Tersebut terhadap Garis Simetri Lipat

Sifat-sifat geometri jajar genjang yang telah dijabarkan di atas secara langsung memengaruhi keberadaan dan jumlah garis simetri lipat. Hanya jajar genjang khusus, yaitu persegi panjang dan belah ketupat (yang juga merupakan jajar genjang), yang memiliki garis simetri lipat. Jajar genjang umum hanya memiliki simetri putar, bukan simetri lipat.

Ilustrasi Pembagian Jajar Genjang oleh Garis Simetri

Bayangkan sebuah persegi panjang. Jika kita menarik garis lurus melalui titik tengah sisi-sisi yang berhadapan, garis tersebut akan membagi persegi panjang menjadi dua bagian yang kongruen, yaitu dua persegi panjang yang identik. Kedua bagian ini merupakan bayangan cermin satu sama lain. Hal yang sama berlaku untuk belah ketupat, tetapi garis simetrinya akan melalui sudut-sudut yang berhadapan. Jajar genjang umum tanpa sudut siku-siku tidak akan memiliki pembagian kongruen seperti ini dengan garis tunggal.

Diagram Garis Simetri Lipat pada Jajar Genjang

Untuk persegi panjang, dua garis simetri lipat dapat digambar, masing-masing melewati titik tengah sisi-sisi yang berhadapan dan tegak lurus terhadap sisi tersebut. Untuk belah ketupat, dua garis simetri lipat dapat digambar, masing-masing melewati dua sudut yang berhadapan. Jajar genjang yang bukan persegi panjang atau belah ketupat tidak memiliki garis simetri lipat.

Perbandingan Simetri Lipat Jajar Genjang dengan Bangun Datar Lain

Dibandingkan dengan bangun datar lain seperti persegi dan lingkaran, jajar genjang memiliki jumlah garis simetri lipat yang lebih sedikit. Persegi memiliki empat garis simetri lipat, sedangkan lingkaran memiliki tak hingga garis simetri lipat. Perbedaan ini mencerminkan tingkat kesimetrisan yang lebih tinggi pada persegi dan lingkaran dibandingkan dengan jajar genjang umum. Persegi panjang dan belah ketupat, sebagai kasus khusus jajar genjang, menunjukkan bagaimana sifat-sifat tertentu dapat meningkatkan jumlah garis simetri lipat.

Menentukan Garis Simetri Lipat Jajar Genjang

Jajar genjang, bangun datar yang didefinisikan oleh dua pasang sisi sejajar, memiliki karakteristik geometri yang menarik, termasuk keberadaan atau ketidakhadiran garis simetri lipat. Memahami bagaimana menentukan garis simetri lipat ini penting dalam berbagai aplikasi, mulai dari desain arsitektur hingga pemecahan masalah geometri tingkat lanjut. Kemampuan untuk mengidentifikasi garis simetri lipat memungkinkan kita untuk memahami sifat-sifat bangun datar ini secara lebih mendalam.

Prosedur Penentuan Garis Simetri Lipat Jajar Genjang

Menentukan garis simetri lipat pada jajar genjang memerlukan pemahaman mendalam tentang sifat-sifat bangun datar ini. Secara sederhana, garis simetri lipat membagi bangun menjadi dua bagian yang kongruen (identik) ketika dilipat. Tidak semua jajar genjang memiliki garis simetri lipat. Hanya jajar genjang khusus, yaitu persegi panjang dan bujur sangkar, yang memiliki garis simetri lipat. Prosedur penentuannya bergantung pada jenis jajar genjang. Untuk jajar genjang yang bukan persegi panjang atau bujur sangkar, tidak ada garis simetri lipat. Untuk persegi panjang, terdapat dua garis simetri lipat yang membagi sisi-sisi yang berhadapan, sementara bujur sangkar memiliki empat garis simetri lipat, dua yang membagi sisi-sisi yang berhadapan dan dua yang membagi diagonalnya.

Penerapan Simetri Lipat Jajar Genjang

Simetri lipat jajar genjang, meskipun mungkin tampak sederhana, memiliki peran yang mengejutkan dalam berbagai aspek kehidupan kita. Dari desain arsitektur yang megah hingga motif batik yang kaya makna, konsep geometris ini menunjukkan pengaruhnya yang luas dan mendalam. Pemahaman tentang simetri lipat jajar genjang bukan hanya penting dalam matematika, tetapi juga membuka wawasan baru dalam seni, kerajinan, dan bahkan ilmu pengetahuan terapan.

Contoh Penerapan Simetri Lipat Jajar Genjang dalam Kehidupan Sehari-hari

Konsep simetri lipat jajar genjang sebenarnya lebih sering kita temui daripada yang kita sadari. Perhatikanlah susunan bata pada dinding bangunan, seringkali mengikuti pola jajar genjang yang menciptakan kekuatan struktural sekaligus estetika visual yang menarik. Contoh lain yang mudah ditemukan adalah pada susunan ubin lantai, terutama pada desain yang modern dan minimalis. Pola-pola ini tak hanya memperindah ruangan, tetapi juga memberikan efisiensi dalam pemakaian material.

Penggunaan Simetri Lipat Jajar Genjang dalam Desain dan Arsitektur

Dalam dunia desain dan arsitektur, simetri lipat jajar genjang sering dimanfaatkan untuk menciptakan efek visual yang dinamis dan modern. Bentuk jajar genjang yang unik memungkinkan terciptanya ruang-ruang yang tidak konvensional dan menarik perhatian. Bangunan-bangunan modern seringkali mengadopsi bentuk-bentuk geometris ini, baik pada fasad maupun pada tata ruang interiornya. Penggunaan material dan pencahayaan yang tepat dapat semakin menonjolkan keindahan simetri lipat jajar genjang dalam desain arsitektur.

Pentingnya Pemahaman Simetri Lipat Jajar Genjang dalam Matematika dan Ilmu Pengetahuan Lainnya

Di luar keindahan estetikanya, pemahaman tentang simetri lipat jajar genjang merupakan fondasi penting dalam berbagai cabang ilmu pengetahuan. Dalam matematika, konsep ini merupakan bagian integral dari geometri, berperan dalam pemahaman transformasi geometri dan analisis ruang. Di bidang fisika dan teknik, prinsip simetri ini diaplikasikan dalam analisis struktur, desain mesin, dan bahkan dalam simulasi komputer.

Ilustrasi Deskriptif Penerapan Simetri Lipat Jajar Genjang dalam Motif Batik

Motif batik, dengan kekayaan dan kerumitannya, seringkali menampilkan simetri lipat jajar genjang yang tersembunyi. Ambil contoh motif batik kawung, dengan pola lingkaran-lingkaran yang tersusun rapat dan membentuk pola jajar genjang tersirat. Keselarasan dan keseimbangan visual yang dihasilkan dari pola ini menciptakan kesan harmonis dan elegan. Simetri lipat berperan dalam menciptakan keseimbangan visual dan kesatuan motif batik tersebut. Perhatikan bagaimana pola-pola tersebut berulang secara teratur, menciptakan ritme dan dinamika visual yang khas.

Contoh Penerapan Simetri Lipat Jajar Genjang dalam Seni dan Kerajinan

Selain batik, simetri lipat jajar genjang juga dapat ditemukan dalam berbagai seni dan kerajinan lainnya. Bayangkan sebuah mosaik dengan potongan-potongan keramik yang tersusun membentuk pola jajar genjang. Permainan warna dan tekstur dapat memperkuat efek visual yang dihasilkan. Kemudian, perhatikan anyaman bambu atau rotan tertentu yang membentuk pola jajar genjang, menunjukkan aplikasi praktis dan estetis dari prinsip geometri ini. Sebuah karya seni ukir kayu dengan pola yang mengikuti bentuk jajar genjang juga akan memperlihatkan keindahan simetri tersebut.

Penutupan Akhir

Kesimpulannya, simetri lipat jajar genjang, meskipun tampak sederhana, menawarkan pemahaman yang lebih dalam tentang konsep simetri dan aplikasinya dalam berbagai bidang. Dari pemahaman dasar tentang garis simetri hingga penerapannya dalam desain dan seni, kajian ini menunjukkan betapa pentingnya memahami konsep geometri dasar. Kemampuan untuk mengidentifikasi dan menganalisis simetri lipat bukan hanya keterampilan matematika, tetapi juga membuka wawasan baru tentang keindahan dan keteraturan di dunia sekitar kita. Dengan demikian, pemahaman mendalam tentang simetri lipat jajar genjang memberikan apresiasi yang lebih terhadap kesederhanaan dan kompleksitas dunia geometri.