Positif kali negatif hasilnya negatif: Sebuah konsep matematika dasar yang ternyata menyimpan misteri dan dampak yang luas, dari transaksi keuangan hingga perubahan suhu yang kita rasakan sehari-hari. Bayangkan keuntungan yang berkurang karena pengeluaran, atau suhu yang melesat turun karena angin dingin. Perkalian bilangan berlawanan tanda ini, yang terlihat sederhana, menawarkan pemahaman yang lebih dalam tentang dunia angka dan aplikasinya di berbagai aspek kehidupan. Memahami konsep ini adalah kunci untuk mengerti bagaimana angka-angka berinteraksi dan mempengaruhi hasil akhir dalam berbagai perhitungan.
Perkalian bilangan positif dan negatif merupakan fondasi aritmatika. Aturannya sederhana: positif dikali positif hasilnya positif, negatif dikali negatif hasilnya positif, sedangkan positif dikali negatif (atau sebaliknya) hasilnya negatif. Konsep ini tidak hanya berlaku dalam buku teks matematika, tetapi juga tercermin dalam berbagai situasi nyata. Dari perhitungan keuangan hingga interpretasi data statistik, memahami interaksi antara bilangan positif dan negatif sangat penting untuk mendapatkan kesimpulan yang akurat dan bermakna.
Perkalian Bilangan Berlawanan Tanda
Perkalian, operasi matematika dasar yang sering kita gunakan sehari-hari, ternyata menyimpan keunikan tersendiri ketika melibatkan bilangan positif dan negatif. Memahami aturan perkalian bilangan berlawanan tanda sangat krusial, tak hanya untuk menyelesaikan soal matematika, tetapi juga untuk berbagai aplikasi di bidang sains, teknologi, hingga ekonomi. Mari kita telusuri seluk-beluknya.
Aturan Perkalian Bilangan Positif dan Negatif
Aturan perkalian bilangan positif dan negatif cukup sederhana namun efektif. Ingatlah prinsip dasar ini: perkalian dua bilangan dengan tanda yang sama menghasilkan bilangan positif, sedangkan perkalian dua bilangan dengan tanda berbeda menghasilkan bilangan negatif. Konsep ini membentuk landasan pemahaman kita tentang operasi perkalian yang melibatkan bilangan berlawanan tanda. Pengaplikasiannya sangat luas, dari menghitung keuntungan dan kerugian finansial hingga menganalisis perubahan suhu.
Contoh Perhitungan Perkalian Bilangan Positif dan Negatif
Mari kita perkuat pemahaman kita dengan beberapa contoh. Dengan memahami pola ini, kita dapat dengan mudah menyelesaikan berbagai perhitungan yang lebih kompleks.
Hasil perkalian positif dan negatif selalu negatif, sebuah konsep dasar matematika yang sederhana namun krusial. Begitu pula dengan sejarah, menarik untuk menelusuri bagaimana permainan bola basket tercipta, seperti yang dijelaskan di permainan bola basket diciptakan pada tanggal tersebut. Analogi ini menunjukkan bahwa sebuah penemuan (positif) bisa lahir dari berbagai tantangan (negatif), menghasilkan dampak signifikan.
Kesimpulannya, layaknya perkalian bilangan, sejarah pun penuh dinamika dimana interaksi antara aspek positif dan negatif menentukan hasil akhirnya.
- Positif x Positif: 5 x 3 = 15
- Negatif x Negatif: (-5) x (-3) = 15
- Positif x Negatif: 5 x (-3) = -15
- Negatif x Positif: (-5) x 3 = -15
Perhatikan bagaimana tanda negatif mempengaruhi hasil akhir. Meskipun angka-angka yang digunakan sama, perubahan tanda dapat menghasilkan hasil yang bertolak belakang. Ini menunjukkan pentingnya ketelitian dalam memperhatikan tanda setiap bilangan yang terlibat dalam perhitungan.
Tabel Perkalian Bilangan Positif dan Negatif
Untuk memudahkan visualisasi, berikut tabel yang merangkum hasil perkalian berbagai kombinasi bilangan positif dan negatif:
| Bilangan 1 | Bilangan 2 | Proses Perkalian | Hasil |
|---|---|---|---|
| 5 | 3 | 5 x 3 | 15 |
| -5 | -3 | (-5) x (-3) | 15 |
| 5 | -3 | 5 x (-3) | -15 |
| -5 | 3 | (-5) x 3 | -15 |
| 10 | -2 | 10 x (-2) | -20 |
| -10 | -2 | (-10) x (-2) | 20 |
Tabel di atas menunjukkan dengan jelas bagaimana tanda setiap bilangan mempengaruhi hasil akhir. Penggunaan tabel ini membantu kita memahami pola dan mempermudah perhitungan.
Ilustrasi Pengaruh Tanda Positif dan Negatif
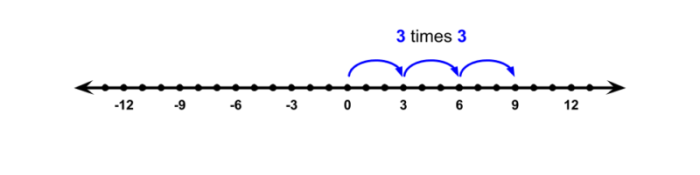
Bayangkan garis bilangan. Bilangan positif berada di sebelah kanan nol, sedangkan bilangan negatif di sebelah kiri. Perkalian dengan bilangan positif seperti “bergerak” searah dengan arah garis bilangan. Sebaliknya, perkalian dengan bilangan negatif seperti “membalikkan” arah. Misalnya, 5 x 3 berarti bergerak 3 langkah ke kanan dari 0, menghasilkan 15. Namun, 5 x (-3) berarti bergerak 3 langkah ke kiri dari 0, menghasilkan -15. Sedangkan (-5) x (-3) berarti membalikkan arah (dari kiri ke kanan) dan bergerak 3 langkah, menghasilkan 15. Ilustrasi ini memberikan gambaran visual yang lebih jelas tentang bagaimana tanda positif dan negatif mempengaruhi hasil perkalian.
Perbedaan Hasil Perkalian Berbagai Kombinasi Bilangan
Perbedaan hasil perkalian antara bilangan positif dengan positif, negatif dengan negatif, dan positif dengan negatif sangat signifikan dan mendasar. Perkalian bilangan positif menghasilkan bilangan positif, mencerminkan penambahan berulang. Perkalian bilangan negatif dengan negatif juga menghasilkan positif, yang dapat diinterpretasikan sebagai pengurangan berulang dari nilai negatif. Namun, perkalian bilangan positif dengan negatif, atau sebaliknya, selalu menghasilkan bilangan negatif, mewakili konsep pengurangan berulang atau penambahan berulang nilai negatif.
Penerapan Perkalian Bilangan Berlawanan Tanda dalam Kehidupan Sehari-hari
Perkalian bilangan positif dan negatif, meskipun tampak abstrak, merupakan konsep matematika yang memiliki aplikasi luas dalam kehidupan nyata. Memahami prinsip ini memudahkan kita dalam menganalisis berbagai situasi keuangan, perubahan suhu, hingga perencanaan proyek. Penerapannya seringkali tak disadari, namun memahami konsep ini memberikan pemahaman yang lebih komprehensif terhadap berbagai dinamika kehidupan sehari-hari.
Konsep perkalian bilangan berlawanan tanda, di mana positif dikalikan negatif menghasilkan negatif dan sebaliknya, memiliki implikasi praktis yang signifikan. Bayangkan bagaimana hal ini memengaruhi perhitungan keuangan, perubahan suhu, atau bahkan perencanaan perjalanan. Dengan memahami prinsip dasar ini, kita dapat melakukan perhitungan yang lebih akurat dan membuat keputusan yang lebih tepat.
Penerapan dalam Konteks Keuangan
Dalam dunia keuangan, perkalian bilangan berlawanan tanda seringkali digunakan untuk menghitung keuntungan dan kerugian. Misalnya, jika sebuah perusahaan mengalami kerugian sebesar Rp 10 juta per bulan selama tiga bulan berturut-turut, maka kerugian totalnya dapat dihitung dengan perkalian: (-Rp 10.000.000) x 3 bulan = -Rp 30.000.000. Angka negatif menunjukkan kerugian, sedangkan angka positif akan menunjukkan keuntungan. Keuntungan dan kerugian bisnis seringkali direpresentasikan dengan bilangan positif dan negatif, dan perkalian digunakan untuk menghitung total dampaknya selama periode tertentu. Contoh lain adalah penghitungan bunga pinjaman, di mana bunga yang harus dibayar direpresentasikan sebagai bilangan negatif (pengurangan saldo) dan jumlah bulan pinjaman direpresentasikan sebagai bilangan positif.
Penerapan dalam Konteks Suhu
Perubahan suhu juga dapat diilustrasikan dengan perkalian bilangan berlawanan tanda. Misalnya, jika suhu turun 2 derajat Celcius per jam selama 5 jam, maka penurunan suhu total adalah (-2°C) x 5 jam = -10°C. Angka negatif menunjukkan penurunan suhu, sedangkan angka positif menunjukkan kenaikan suhu. Ini menunjukkan bagaimana perkalian bilangan positif dan negatif dapat digunakan untuk menghitung perubahan suhu secara akurat, baik kenaikan maupun penurunan. Contoh lain, perhitungan pendinginan suatu objek dengan laju penurunan suhu konstan.
Dalam matematika, positif dikalikan negatif hasilnya negatif; sebuah rumus sederhana namun berdampak luas. Begitu pula dalam dunia musik, kontras antara nada-nada ceria dan melodi yang melankolis bisa menghasilkan emosi yang mendalam. Perhatikan bagaimana tangga lagu yang memiliki sifat sedih dan haru, seperti yang dijelaskan di bagaimana tangga lagu yang memiliki sifat sedih dan haru , seringkali menggunakan interval-interval minor yang menciptakan nuansa pilu.
Ini ibarat perkalian positif (keindahan aransemen) dengan negatif (emosi sedih), menghasilkan sebuah karya yang membekas di hati pendengar. Hasil akhirnya, meskipun negatif secara emosional, justru memiliki nilai positif secara artistik.
Tiga Skenario Tambahan Perkalian Bilangan Positif dan Negatif, Positif kali negatif hasilnya
- Perhitungan Stok Barang: Sebuah toko mengalami penurunan stok 5 unit barang per hari selama 3 hari. Perhitungan penurunan total stok adalah (-5 unit/hari) x 3 hari = -15 unit. Angka negatif menunjukkan berkurangnya stok.
- Penggunaan Baterai: Sebuah perangkat elektronik kehilangan daya baterai 10% per jam selama 2 jam penggunaan. Pengurangan daya baterai total adalah (-10%) x 2 jam = -20%. Angka negatif menunjukkan penurunan persentase daya baterai.
- Perencanaan Anggaran: Seorang individu merencanakan pengeluaran -Rp 50.000 per hari untuk transportasi selama 5 hari. Total pengeluaran transportasi adalah (-Rp 50.000/hari) x 5 hari = -Rp 250.000. Angka negatif menunjukkan pengurangan saldo uang.
Contoh Soal Cerita dan Penyelesaiannya
Sebuah perusahaan mengalami keuntungan Rp 20 juta per bulan selama 2 bulan pertama, kemudian mengalami kerugian Rp 15 juta per bulan selama 3 bulan berikutnya. Berapakah keuntungan atau kerugian total perusahaan selama 5 bulan tersebut?
Penyelesaian:
Keuntungan bulan 1 dan 2: (Rp 20.000.000) x 2 = Rp 40.000.000
Kerugian bulan 3, 4, dan 5: (-Rp 15.000.000) x 3 = -Rp 45.000.000
Keuntungan/Kerugian total: Rp 40.000.000 + (-Rp 45.000.000) = -Rp 5.000.000
Hasil perhitungan menunjukkan perusahaan mengalami kerugian total sebesar Rp 5.000.000 selama 5 bulan tersebut.
Pengaruh pada Hasil Akhir Perkalian
Perkalian, operasi matematika dasar, tak hanya melibatkan pengulangan penjumlahan. Pemahaman mendalam tentang perkalian menuntut pemahaman yang cermat terhadap peran tanda negatif. Tanda negatif, seringkali dianggap sebagai detail kecil, justru memegang peranan krusial dalam menentukan hasil akhir. Ketelitian dalam memperhatikan tanda-tanda ini akan menentukan keakuratan perhitungan dan menghindari kesalahan yang berdampak signifikan, khususnya dalam aplikasi matematika yang lebih kompleks.
Pengaruh tanda negatif dalam perkalian sangat signifikan. Ia mengubah nilai hasil akhir, membalikkan arah dari positif ke negatif atau sebaliknya. Ini bukan sekadar perubahan angka, melainkan perubahan makna dalam konteks masalah yang dipecahkan. Kegagalan memahami aturan tanda dalam perkalian dapat menghasilkan kesalahan interpretasi yang serius, mengarah pada kesimpulan yang salah dan keputusan yang keliru.
Perubahan Nilai Akibat Tanda Negatif
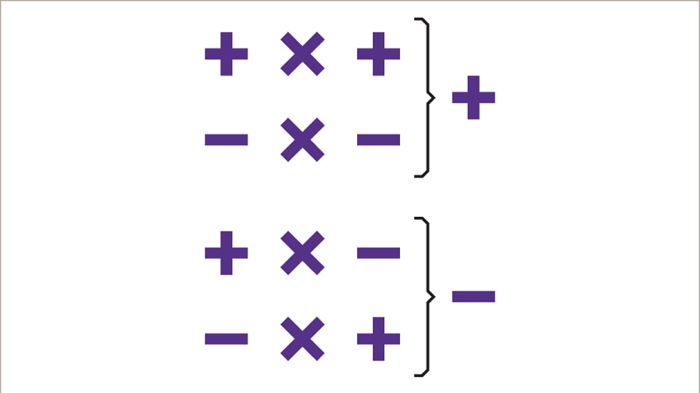
Perkalian bilangan dengan tanda yang berbeda menghasilkan hasil yang berbeda pula. Perkalian dua bilangan positif selalu menghasilkan bilangan positif. Sebaliknya, perkalian dua bilangan negatif menghasilkan bilangan positif. Namun, perkalian bilangan positif dengan bilangan negatif, atau sebaliknya, selalu menghasilkan bilangan negatif. Pola ini konsisten dan mendasar dalam aljabar dan kalkulus.
Dalam matematika, positif kali negatif hasilnya negatif; fakta sederhana yang seringkali luput dari perhatian. Begitu pula dengan sejarah, perjuangan kemerdekaan Indonesia, yang penuh dinamika dan pengorbanan, menghasilkan sebuah pernyataan monumental: Proklamasi Kemerdekaan. Pertanyaannya, mengapa dokumen tersebut diakui secara legal dan resmi? Untuk memahami legalitasnya, kita perlu menelaah lebih dalam, seperti yang dijelaskan secara rinci di mengapa proklamasi merupakan pernyataan yang legal dan resmi.
Intinya, prosesnya rumit, sebagaimana perkalian bilangan positif dan negatif menghasilkan sebuah nilai yang tak selalu intuitif. Namun, hasilnya, sebuah tonggak sejarah yang tak terbantahkan.
- Positif x Positif = Positif
- Negatif x Negatif = Positif
- Positif x Negatif = Negatif
- Negatif x Positif = Negatif
Pentingnya Memperhatikan Tanda Bilangan
Perhatikan dengan seksama tanda setiap bilangan sebelum melakukan perkalian. Kesalahan kecil dalam memperhatikan tanda dapat menyebabkan hasil yang sepenuhnya berbeda dan berdampak signifikan, terutama dalam perhitungan yang lebih kompleks. Ketelitian adalah kunci keberhasilan dalam matematika.
Contoh Pengaruh Perubahan Tanda
Mari kita lihat beberapa contoh konkret. Jika kita mengalikan 5 dengan 3, hasilnya adalah 15 (positif). Namun, jika kita mengalikan -5 dengan 3, hasilnya menjadi -15 (negatif). Begitu pula, -5 dikalikan dengan -3 menghasilkan 15 (positif). Perubahan tanda pada salah satu bilangan atau keduanya secara langsung mempengaruhi tanda dan nilai hasil akhir. Perbedaan ini bukan hanya sekedar perubahan angka, tetapi juga perubahan signifikansi dalam konteks permasalahan yang dihadapi.
| Perkalian | Hasil |
|---|---|
| 5 x 3 | 15 |
| -5 x 3 | -15 |
| 5 x -3 | -15 |
| -5 x -3 | 15 |
Implikasi Pengabaian Tanda Bilangan
Mengabaikan tanda bilangan dalam perkalian, terutama dalam perhitungan yang melibatkan bilangan berlawanan tanda, dapat berakibat fatal. Ini bisa menyebabkan kesalahan dalam perhitungan keuangan, peramalan ilmiah, bahkan dalam perencanaan proyek sederhana. Akurasi dalam memperhatikan tanda-tanda ini menjadi sangat penting untuk memastikan hasil yang valid dan dapat diandalkan. Ketidaktelitian ini bisa berujung pada kesalahan besar dengan konsekuensi yang signifikan.
Hubungan Perkalian Bilangan Berlawanan Tanda dengan Operasi Matematika Lain
Perkalian bilangan positif dan negatif merupakan konsep dasar dalam aljabar yang memiliki keterkaitan erat dengan operasi matematika lainnya seperti penjumlahan, pengurangan, dan pembagian. Memahami hubungan ini krusial untuk menyelesaikan berbagai permasalahan matematika, baik yang sederhana maupun kompleks. Kemampuan menguasai konsep ini akan membuka jalan untuk memecahkan persamaan yang lebih rumit dan mengaplikasikannya dalam berbagai bidang, mulai dari ilmu fisika hingga ekonomi.
Perkalian Bilangan Berlawanan Tanda dan Penjumlahan/Pengurangan
Perkalian bilangan berlawanan tanda dapat diinterpretasikan sebagai penjumlahan atau pengurangan berulang. Misalnya, -3 x 4 dapat dipahami sebagai penjumlahan -3 sebanyak 4 kali, menghasilkan -12. Sebaliknya, 3 x -4 dapat dilihat sebagai pengurangan 3 sebanyak 4 kali, yang juga menghasilkan -12. Konsep ini memperlihatkan kesinambungan dan keterkaitan erat antara perkalian dengan operasi penjumlahan dan pengurangan. Ini merupakan fondasi penting dalam memahami sifat distributif perkalian terhadap penjumlahan dan pengurangan.
Perkalian Bilangan Berlawanan Tanda dan Pembagian
Hubungan antara perkalian dan pembagian bersifat invers. Jika -6 x 2 = -12, maka -12 / 2 = -6, atau -12 / -6 = 2. Dengan demikian, perkalian bilangan berlawanan tanda dapat digunakan untuk menyelesaikan soal pembagian yang melibatkan bilangan negatif. Ini juga menunjukkan bahwa operasi pembagian merupakan kebalikan dari perkalian, dan pemahaman terhadap salah satu operasi akan mempermudah pemahaman terhadap operasi lainnya.
Langkah-Langkah Menyelesaikan Persamaan yang Melibatkan Perkalian Bilangan Berlawanan Tanda dan Operasi Lain
- Identifikasi semua bilangan positif dan negatif dalam persamaan.
- Lakukan perkalian bilangan berlawanan tanda terlebih dahulu, perhatikan aturan tanda (positif x negatif = negatif, negatif x negatif = positif).
- Lakukan penjumlahan dan pengurangan sesuai dengan urutan operasi (prioritas perkalian dan pembagian sebelum penjumlahan dan pengurangan).
- Sederhanakan hasil hingga diperoleh solusi akhir.
Contoh Soal: Perkalian, Penjumlahan, dan Pengurangan Bilangan Positif dan Negatif
Misalnya, selesaikan persamaan berikut: (5 x -2) + (-3) – (-4) = ?
Penyelesaian:
- Perkalian terlebih dahulu: 5 x -2 = -10
- Persamaan menjadi: -10 + (-3) – (-4)
- Sederhanakan tanda: -10 – 3 + 4
- Hitung penjumlahan dan pengurangan: -10 – 3 = -13, kemudian -13 + 4 = -9
- Jadi, hasilnya adalah -9
Ringkasan Hubungan Operasi Matematika
Perkalian bilangan berlawanan tanda merupakan operasi yang terintegrasi dengan penjumlahan, pengurangan, dan pembagian. Memahami aturan tanda dan urutan operasi merupakan kunci untuk menyelesaikan persamaan yang melibatkan operasi-operasi tersebut. Konsep ini fundamental dalam aljabar dan memiliki aplikasi luas dalam berbagai bidang.
Ringkasan Akhir: Positif Kali Negatif Hasilnya
Kesimpulannya, memahami aturan perkalian bilangan berlawanan tanda—positif kali negatif hasilnya negatif—bukan sekadar kemampuan matematika dasar, tetapi juga kunci untuk menafsirkan dunia sekitar kita. Dari perhitungan keuangan hingga prediksi perubahan iklim, konsep ini memberikan kerangka kerja yang penting untuk menganalisis dan memahami berbagai fenomena. Kemampuan untuk menerapkan konsep ini dengan tepat akan membantu dalam pengambilan keputusan yang lebih terinformasi dan efektif dalam berbagai aspek kehidupan.
 TendikPedia Informasi Mengenai Pendidikan yang Akurat dan Terpercaya
TendikPedia Informasi Mengenai Pendidikan yang Akurat dan Terpercaya



