Negatif kali positif sama dengan negatif. Konsep sederhana ini, yang sering dianggap remeh, ternyata mendasari banyak perhitungan kompleks dalam berbagai bidang. Dari rumus fisika yang mengungkap misteri alam semesta hingga laporan keuangan perusahaan raksasa, operasi perkalian bilangan berlawanan tanda ini berperan krusial. Memahami konsep ini dengan tuntas membuka pintu untuk menguasai matematika yang lebih lanjut, dan bahkan membantu dalam pengambilan keputusan finansial yang lebih cerdas. Perjalanan kita kali ini akan mengupas tuntas misteri di balik tanda minus yang misterius ini.
Perkalian bilangan berlawanan tanda, khususnya negatif kali positif, merupakan fondasi aritmatika yang mendasari pemahaman aljabar, kalkulus, dan berbagai cabang matematika lainnya. Menguasai konsep ini berarti membuka jalan menuju pemahaman yang lebih dalam tentang bagaimana angka-angka berinteraksi dan membentuk pola-pola yang kompleks. Dengan ilustrasi yang jelas dan contoh-contoh praktis dari kehidupan sehari-hari, kita akan menjelajahi konsep ini secara menyeluruh, mulai dari perkalian bilangan bulat hingga penerapannya dalam konteks yang lebih luas, seperti fisika, ekonomi, dan pemrograman komputer.
Perkalian Bilangan Berlawanan Tanda
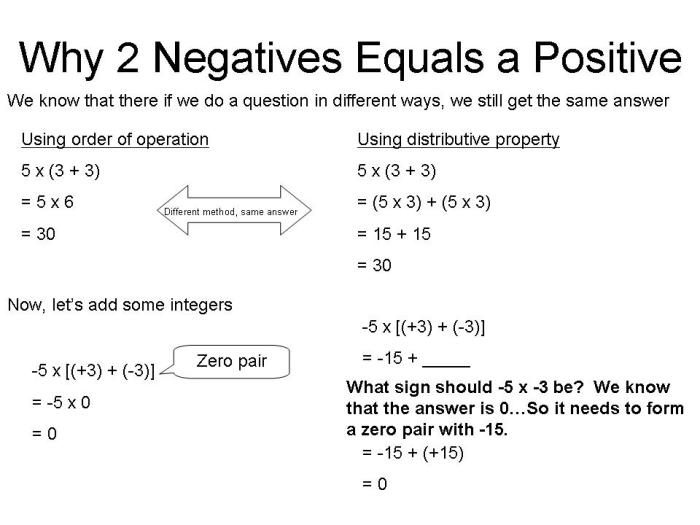
Operasi perkalian, yang sering dianggap sederhana, menyimpan keunikan tersendiri ketika melibatkan bilangan positif dan negatif. Memahami aturan perkalian bilangan berlawanan tanda krusial, bukan hanya dalam matematika dasar, tetapi juga dalam berbagai aplikasi, mulai dari pemrograman komputer hingga analisis keuangan. Perhitungan yang melibatkan untung dan rugi, misalnya, sangat bergantung pada pemahaman yang tepat tentang konsep ini. Kesalahan kecil dalam memahami aturan ini dapat berdampak besar pada hasil akhir, mengakibatkan interpretasi data yang keliru.
Aturan Perkalian Bilangan Positif dan Negatif
Aturan dasar perkalian bilangan berlawanan tanda cukup mudah diingat: perkalian dua bilangan dengan tanda yang sama (positif x positif atau negatif x negatif) menghasilkan bilangan positif. Sebaliknya, perkalian dua bilangan dengan tanda berbeda (positif x negatif atau negatif x positif) akan menghasilkan bilangan negatif. Konsep ini membentuk landasan untuk perhitungan yang lebih kompleks yang melibatkan bilangan bulat, desimal, bahkan variabel aljabar.
Negatif kali positif sama dengan negatif, sebuah konsep matematika dasar yang sederhana. Namun, konsep ini bisa dianalogikan dengan banyak hal, misalnya dinamika kehidupan seorang guru. Ambil contoh perjalanan spiritual guru Ki Prana Lewu , yang penuh lika-liku, menunjukkan bagaimana pengalaman negatif (cobaan) dikalikan dengan positif (keuletan dan keimanan) menghasilkan dampak negatif yang justru membentuk karakter kuat.
Intinya, meski hasilnya negatif, prosesnya membentuk transformasi. Kembali ke matematika, negatif kali positif tetap sama dengan negatif, tetapi nilai negatif itu sendiri bisa memiliki makna yang jauh lebih kompleks.
Contoh Perkalian Bilangan Bulat Positif dan Negatif
Mari kita lihat beberapa contoh untuk mengilustrasikan aturan ini. Perkalian 5 x 3 menghasilkan 15 (positif x positif = positif). Sementara itu, perkalian -5 x 3 menghasilkan -15 (negatif x positif = negatif), dan 5 x -3 juga menghasilkan -15 (positif x negatif = negatif). Sedangkan -5 x -3 menghasilkan 15 (negatif x negatif = positif). Perbedaan tanda pada bilangan yang dikalikan secara langsung memengaruhi tanda hasil akhirnya.
Tabel Perkalian Berbagai Kombinasi Bilangan
Untuk memperjelas, berikut tabel yang merangkum hasil perkalian berbagai kombinasi bilangan, termasuk nol:
| Bilangan Pertama | Bilangan Kedua | Operasi | Hasil |
|---|---|---|---|
| 5 | 3 | 5 x 3 | 15 |
| -5 | 3 | -5 x 3 | -15 |
| 5 | -3 | 5 x -3 | -15 |
| -5 | -3 | -5 x -3 | 15 |
| 0 | 3 | 0 x 3 | 0 |
| -7 | 0 | -7 x 0 | 0 |
Perkalian Bilangan Desimal Positif dan Negatif
Aturan yang sama berlaku untuk bilangan desimal. Misalnya, 2.5 x -1.2 = -3. Hasilnya negatif karena perkalian melibatkan satu bilangan positif dan satu bilangan negatif. Begitu pula, -2.5 x -1.2 = 3, menghasilkan bilangan positif karena kedua bilangan yang dikalikan bernilai negatif. Proses perhitungannya sama seperti perkalian bilangan bulat, hanya saja melibatkan angka desimal.
Contoh Soal Cerita Perkalian Bilangan Berlawanan Tanda
Sebuah perusahaan mengalami kerugian sebesar Rp 2.000.000 per bulan selama tiga bulan berturut-turut. Untuk menghitung total kerugian, kita perlu mengalikan kerugian per bulan dengan jumlah bulan: -2.000.000 x 3 = -6.000.000. Hasil negatif menunjukkan total kerugian perusahaan selama tiga bulan tersebut sebesar Rp 6.000.000. Contoh ini menunjukkan bagaimana perkalian bilangan berlawanan tanda diterapkan dalam konteks dunia nyata.
Negatif kali positif sama dengan negatif; konsep matematika dasar yang sering kita anggap sederhana. Namun, pernahkah Anda berpikir mengapa, misalnya, lingkaran selalu berbentuk lingkaran? Pertanyaan ini mungkin tampak tak berkaitan, namun menarik untuk dikaji lebih lanjut, terutama jika kita mencari jawabannya di mengapa bentuknya lingkaran. Kembali ke konsep negatif kali positif, kesederhanaannya menunjukkan betapa fundamentalnya konsep tersebut dalam matematika, sebagaimana bentuk lingkaran yang konsisten menunjukkan prinsip geometri yang tetap.
Penerapan Perkalian Bilangan Berlawanan Tanda dalam Matematika
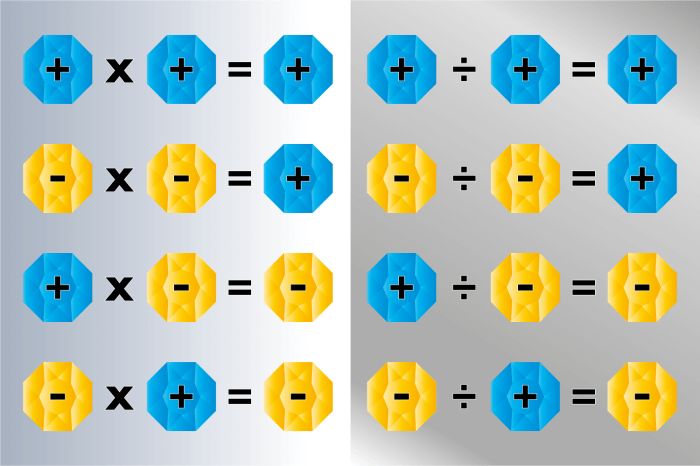
Perkalian bilangan positif dan negatif, meskipun tampak sederhana, merupakan konsep fundamental dalam matematika yang memiliki implikasi luas dalam berbagai bidang, mulai dari aljabar dasar hingga kalkulus tingkat lanjut. Memahami aturan perkalian ini sangat krusial untuk menyelesaikan berbagai permasalahan matematika dan bahkan dalam aplikasi di dunia nyata, seperti perhitungan keuangan atau analisis data. Kemampuan untuk dengan tepat menghitung hasil perkalian bilangan berlawanan tanda merupakan kunci untuk menguasai berbagai konsep matematika yang lebih kompleks.
Aturan dasar perkalian bilangan berlawanan tanda adalah: positif dikalikan positif hasilnya positif, negatif dikalikan negatif hasilnya positif, dan positif dikalikan negatif (atau sebaliknya) hasilnya negatif. Konsep ini, yang tampak sederhana, membentuk landasan bagi pemahaman yang lebih dalam tentang aljabar, geometri, dan bidang matematika lainnya.
Negatif kali positif sama dengan negatif, sebuah konsep dasar matematika yang sederhana namun mendasar. Konsep ini, sebagaimana kita memahami hukum fisika dasar, memiliki implikasi yang luas. Bayangkan, pergerakan kita sehari-hari, seperti yang dijelaskan di berjalan berlari dan melompat termasuk gerak , bisa dianalogikan sebagai interaksi antara gaya-gaya yang berlawanan arah. Hasil akhirnya, pergerakan itu sendiri, bisa diinterpretasikan sebagai hasil perkalian gaya-gaya tersebut; jika satu gaya negatif (misalnya, hambatan udara), dan lainnya positif (misalnya, dorongan kaki), maka hasilnya adalah pergerakan yang tetap terpengaruh negatif, meskipun tetap terjadi.
Kembali ke matematika, negatif kali positif tetap sama dengan negatif, sebagaimana kompleksitas interaksi gaya dalam kehidupan nyata.
Perkalian Bilangan Berlawanan Tanda dalam Aljabar
Penggunaan perkalian bilangan berlawanan tanda dalam aljabar sangatlah penting. Konsep ini menjadi dasar dalam penyederhanaan ekspresi aljabar, manipulasi persamaan, dan pemecahan masalah. Misalnya, dalam menyederhanakan ekspresi -3(2x – 5), kita perlu mengalikan -3 dengan masing-masing suku dalam kurung, menghasilkan -6x + 15. Ketepatan dalam menerapkan aturan tanda menentukan keakuratan hasil akhir. Kesalahan kecil dalam tanda dapat menyebabkan penyimpangan yang signifikan dalam perhitungan.
Perkalian Bilangan Berlawanan Tanda dalam Penyelesaian Persamaan Linear
Dalam menyelesaikan persamaan linear, perkalian bilangan berlawanan tanda sering digunakan untuk mengisolasi variabel. Misalnya, untuk menyelesaikan persamaan -2x = 6, kita perlu membagi kedua sisi persamaan dengan -2. Proses ini melibatkan pembagian dengan bilangan negatif, yang secara esensial adalah perkalian dengan kebalikannya (yaitu, -1/2). Hasilnya, kita mendapatkan x = -3. Pemahaman yang tepat tentang perkalian bilangan berlawanan tanda memastikan kita dapat memanipulasi persamaan dengan benar dan menemukan solusi yang akurat.
Penerapan dalam Geometri: Luas dan Volume
Konsep perkalian bilangan berlawanan tanda juga muncul dalam geometri, khususnya dalam perhitungan luas dan volume. Bayangkan sebuah persegi panjang dengan panjang -4 satuan dan lebar 3 satuan. Luas persegi panjang dihitung dengan mengalikan panjang dan lebarnya. Dalam hal ini, luasnya adalah (-4) x 3 = -12 satuan persegi. Nilai negatif menunjukkan interpretasi kontekstual, misalnya, mungkin mewakili suatu besaran yang berlawanan arah. Penting untuk memahami bahwa tanda negatif dalam konteks ini tidak selalu menunjukkan kesalahan perhitungan, tetapi dapat merepresentasikan arah atau orientasi suatu besaran dalam ruang. Hal yang sama juga berlaku dalam perhitungan volume bangun ruang.
Langkah-langkah Menyelesaikan Persamaan yang Melibatkan Perkalian Bilangan Positif dan Negatif
- Identifikasi operasi perkalian yang melibatkan bilangan positif dan negatif dalam persamaan.
- Terapkan aturan perkalian bilangan berlawanan tanda: positif dikalikan positif = positif; negatif dikalikan negatif = positif; positif dikalikan negatif = negatif.
- Sederhanakan persamaan dengan melakukan operasi perkalian.
- Jika perlu, gunakan sifat komutatif dan asosiatif perkalian untuk memudahkan perhitungan.
- Lanjutkan penyelesaian persamaan dengan menggunakan metode aljabar yang sesuai, seperti penjumlahan, pengurangan, atau pembagian.
- Verifikasi solusi dengan mensubstitusikan nilai variabel yang diperoleh ke dalam persamaan awal.
Contoh Penyelesaian Persamaan
Mari selesaikan persamaan -5x + 10 = -15.
- Kurangi 10 dari kedua sisi: -5x = -25
- Bagi kedua sisi dengan -5: x = 5
Dalam contoh ini, kita mengalikan -5 dengan x dan kemudian membagi -25 dengan -5. Penggunaan aturan perkalian bilangan berlawanan tanda memastikan kita mendapatkan solusi yang tepat, yaitu x = 5. Perhatikan bahwa hasil akhir positif, meskipun proses penyelesaian melibatkan bilangan negatif.
Ilustrasi Konsep Perkalian Bilangan Positif dan Negatif
Perkalian bilangan positif dan negatif, meskipun tampak sederhana, menyimpan konsep yang perlu dipahami dengan jelas. Konsep ini seringkali menjadi batu sandungan bagi siswa, bahkan hingga ke jenjang pendidikan yang lebih tinggi. Memahami konsep ini dengan baik, bukan hanya sekadar menghafal aturan, melainkan juga mengerti logika di baliknya. Visualisasi melalui gambar dan ilustrasi menjadi kunci untuk menguasai konsep ini secara menyeluruh.
Berikut ini beberapa ilustrasi yang akan membantu Anda memahami perkalian bilangan positif dan negatif, mulai dari penggunaan garis bilangan hingga penerapannya dalam konteks kehidupan sehari-hari.
Perkalian Negatif Kali Positif Menggunakan Garis Bilangan, Negatif kali positif sama dengan
Ilustrasi ini menggunakan garis bilangan sebagai alat bantu visual. Misalnya, perhitungan -2 x 3. Kita mulai dari angka 0 pada garis bilangan. Karena angka 3 positif, kita bergerak ke arah kanan (arah positif) sebanyak tiga kali, dengan setiap langkah besarnya 2 unit, namun karena angka -2 negatif, setiap langkah kita akan menuju ke arah negatif (kiri). Hasil akhirnya adalah -6, yang ditunjukkan oleh posisi akhir pada garis bilangan. Dengan demikian, perkalian negatif kali positif menghasilkan nilai negatif.
Perkalian Negatif Kali Negatif Menggunakan Garis Bilangan
Ilustrasi ini serupa dengan sebelumnya, namun dengan operasi yang berbeda. Ambil contoh -2 x -3. Kita mulai dari angka 0. Karena angka -3 negatif, kita akan bergerak ke arah kiri (arah negatif) sebanyak tiga kali. Namun, karena angka -2 juga negatif, setiap langkah bernilai 2 unit ke arah berlawanan dari arah negatif, yaitu ke arah positif (kanan). Hasil akhirnya adalah +6, yang menunjukkan bahwa perkalian negatif kali negatif menghasilkan nilai positif. Ini mungkin tampak kontradiktif pada awalnya, tetapi ilustrasi ini membantu memvisualisasikan konsep tersebut.
Representasi Perkalian Negatif Kali Positif dalam Luas Persegi Panjang
Bayangkan sebuah persegi panjang. Misalkan panjangnya -4 unit (nilai negatif, bisa diartikan sebagai pengukuran ke arah kiri dari titik acuan) dan lebarnya 2 unit (nilai positif). Luas persegi panjang dihitung dengan mengalikan panjang dan lebar. (-4) x 2 = -8. Luas negatif dapat diinterpretasikan sebagai representasi area yang “hilang” atau “berkurang” dari titik acuan. Konsep ini penting dalam beberapa aplikasi matematika dan fisika.
Perkalian Negatif Kali Positif dalam Konteks Penurunan Suhu
Pertimbangkan skenario penurunan suhu. Misalkan suhu turun 3 derajat Celcius setiap jam selama 2 jam. Ini dapat direpresentasikan sebagai -3 derajat/jam x 2 jam = -6 derajat Celcius. Hasil negatif menunjukkan penurunan suhu sebesar 6 derajat Celcius dari suhu awal. Ilustrasi ini menunjukkan penerapan perkalian negatif kali positif dalam konteks dunia nyata yang mudah dipahami. Ini menggambarkan bagaimana konsep matematika tersebut dapat digunakan untuk memodelkan perubahan kuantitatif.
Analogi dan Perumpamaan Perkalian Bilangan Berlawanan Tanda: Negatif Kali Positif Sama Dengan
Memahami perkalian bilangan negatif dan positif seringkali menjadi tantangan, terutama bagi pemula. Konsep ini, yang tampak abstrak, dapat disederhanakan dengan analogi dan perumpamaan yang relevan dengan kehidupan sehari-hari. Dengan demikian, pemahaman akan menjadi lebih intuitif dan mudah diingat. Berikut beberapa analogi dan perumpamaan yang dapat membantu memahami konsep perkalian bilangan negatif dan positif.
Perkalian Negatif Kali Positif: Hutang dan Pembayaran
Bayangkan Anda memiliki hutang sebesar Rp 50.000 (negatif). Jika Anda membayar hutang tersebut sebanyak 3 kali (positif), maka total hutang Anda berkurang sebesar Rp 150.000. Dengan demikian, 3 (positif) x (-Rp 50.000) = -Rp 150.000. Pengurangan hutang di sini direpresentasikan sebagai angka negatif, menunjukkan bahwa jumlah hutang semakin berkurang. Ini merupakan analogi sederhana yang menghubungkan operasi matematika dengan situasi keuangan yang familiar.
Perumpamaan Perkalian Negatif Kali Positif: Suhu dan Waktu
Suhu udara di suatu daerah turun 5 derajat Celcius setiap jam (negatif) selama 3 jam (positif). Perubahan suhu total adalah penurunan 15 derajat Celcius. Dengan demikian, 3 (positif) x (-5 derajat Celcius) = -15 derajat Celcius. Analogi ini menggambarkan bagaimana suatu besaran negatif yang berulang kali terjadi dalam waktu positif akan menghasilkan total negatif yang lebih besar.
Analogi Perkalian Negatif Kali Negatif: Pembalikan Arah dan Tindakan
Perkalian negatif kali negatif dapat dianalogikan sebagai pembalikan arah dan tindakan. Bayangkan Anda berjalan mundur (negatif) dengan kecepatan 5 meter per detik (negatif). Jika Anda melakukan ini selama 2 detik (negatif), maka posisi Anda sebenarnya akan maju 10 meter. Ini karena pembalikan arah dan tindakan menghasilkan efek yang berlawanan. Jadi, (-5 meter/detik) x (-2 detik) = 10 meter.
Perumpamaan Perkalian Negatif Kali Negatif: Penambahan Keuntungan
Sebuah perusahaan mengalami kerugian sebesar Rp 10 juta per bulan selama dua bulan berturut-turut (negatif). Namun, strategi baru yang diterapkan menghasilkan peningkatan keuntungan sebesar Rp 20 juta per bulan selama dua bulan tersebut (negatif). Akibatnya, perusahaan mengalami peningkatan laba total sebesar Rp 20 juta. Perubahan dari kerugian ke keuntungan direpresentasikan sebagai perkalian dua bilangan negatif, yang menghasilkan nilai positif.
Analogi Sederhana untuk Anak-Anak: Mainan dan Kotak
Bayangkan Anda memiliki 3 kotak mainan (positif). Setiap kotak memiliki 2 mainan yang hilang (negatif). Untuk mengetahui total mainan yang hilang, kita hitung 3 (positif) x (-2 mainan) = -6 mainan. Ini menunjukkan bahwa total mainan yang hilang adalah 6 buah. Jika kemudian Anda menemukan kembali 2 kotak mainan (negatif) yang masing-masing berisi 3 mainan yang hilang (negatif), maka total mainan yang ditemukan adalah 6 buah (-2 x -3 = 6).
Contoh Penerapan Negatif Kali Positif
Konsep perkalian bilangan negatif dan positif, meskipun sederhana, memiliki implikasi luas di berbagai bidang. Pemahaman yang mendalam tentang bagaimana tanda negatif mengubah hasil perkalian sangat krusial, baik dalam perhitungan fisika maupun analisis keuangan. Ketidaktelitian dalam penerapan konsep ini dapat berakibat fatal, mulai dari kesalahan perhitungan sederhana hingga kerugian finansial yang signifikan. Berikut beberapa contoh penerapannya dalam berbagai disiplin ilmu.
Penerapan dalam Ilmu Fisika
Dalam fisika, khususnya mekanika, konsep ini sering muncul dalam perhitungan gaya dan percepatan. Misalnya, sebuah benda yang bergerak ke arah timur (dianggap positif) dikenai gaya gesekan ke arah barat (dianggap negatif). Hasil perkalian gaya gesek dengan perpindahan benda akan menghasilkan kerja yang bernilai negatif, menunjukkan energi yang hilang karena gesekan. Semakin besar gaya gesek, semakin besar energi yang hilang. Percepatan juga dapat dihitung dengan mempertimbangkan gaya yang berlawanan arah. Jika gaya dorong positif dan gaya hambat negatif, percepatan bersih akan menjadi selisih antara keduanya, yang dapat bernilai positif atau negatif tergantung besarnya masing-masing gaya. Sebuah roket yang meluncur ke atas, misalnya, mengalami gaya gravitasi ke bawah (negatif) yang melawan gaya dorong mesin (positif). Percepatan roket ditentukan oleh selisih kedua gaya tersebut.
Penerapan dalam Pemrograman Komputer
Dalam pemrograman, perkalian bilangan negatif sering digunakan dalam berbagai algoritma dan manipulasi data. Sebagai contoh, dalam representasi data numerik, bilangan negatif diwakili menggunakan komplemen dua. Operasi perkalian dengan bilangan negatif melibatkan perubahan bit yang rumit, tetapi hasilnya selalu konsisten dengan aturan perkalian bilangan negatif dan positif. Berikut contoh sederhana dalam bahasa Python:
x = 5
y = -2
hasil = x * y
print(hasil) # Output: -10
Contoh lain adalah dalam pengolahan citra digital, di mana nilai piksel negatif dapat mewakili tingkat kecerahan atau warna yang lebih rendah dari nilai standar. Operasi perkalian dengan nilai negatif dapat digunakan untuk melakukan inversi warna atau penyesuaian kontras.
Penerapan dalam Bidang Keuangan
Dalam dunia keuangan, perkalian bilangan negatif sering digunakan untuk menghitung kerugian. Jika pendapatan suatu perusahaan dinyatakan sebagai bilangan positif, maka kerugian akan direpresentasikan sebagai bilangan negatif. Perkalian kerugian (negatif) dengan jumlah unit yang terjual akan menghasilkan total kerugian yang lebih besar. Sebagai contoh, jika sebuah perusahaan mengalami kerugian Rp 10.000 per unit dan menjual 100 unit, total kerugiannya adalah Rp 1.000.000 ( -10.000 x 100 = -1.000.000).
Penerapan dalam Bidang Ekonomi
Konsep ini berperan penting dalam analisis ekonomi makro, khususnya dalam menghitung dampak kebijakan fiskal. Misalnya, pengurangan pajak (dianggap negatif karena mengurangi penerimaan negara) dapat berdampak positif pada konsumsi masyarakat dan investasi, sehingga meningkatkan pertumbuhan ekonomi. Namun, dampak positif tersebut mungkin tidak selalu sebanding dengan pengurangan penerimaan negara, yang dihitung dengan mengalikan nilai pengurangan pajak (negatif) dengan efek pengganda ekonomi. Perlu analisis yang cermat untuk memastikan kebijakan fiskal tersebut memberikan dampak positif secara keseluruhan.
Penerapan dalam Bidang Akuntansi
Dalam akuntansi, pengurangan aset seringkali diwakilkan dengan angka negatif. Misalnya, penyusutan aset tetap akan mengurangi nilai aset tersebut dari waktu ke waktu. Nilai penyusutan ini dicatat sebagai angka negatif dalam laporan keuangan. Jika nilai penyusutan suatu aset sebesar Rp 1.000.000 per tahun, selama 5 tahun, maka total penyusutannya adalah Rp 5.000.000 ( -1.000.000 x 5 = -5.000.000). Ini mencerminkan penurunan nilai aset tersebut dalam neraca perusahaan.
Kesimpulan
Memahami konsep “negatif kali positif sama dengan negatif” bukan sekadar menghafal rumus, melainkan memahami logika di baliknya. Dengan analogi yang tepat dan pemahaman visual, konsep ini menjadi intuitif dan mudah diingat. Dari hutang dan pembayaran hingga perubahan suhu, konsep ini tertanam dalam realitas kita. Menguasainya membuka jalan menuju pemahaman yang lebih dalam tentang dunia angka dan aplikasinya dalam berbagai disiplin ilmu. Perjalanan kita menguak misteri tanda minus telah berakhir, namun pemahaman yang kita peroleh akan terus bermanfaat dalam menghadapi tantangan numerik di masa depan.
 TendikPedia Informasi Mengenai Pendidikan yang Akurat dan Terpercaya
TendikPedia Informasi Mengenai Pendidikan yang Akurat dan Terpercaya